Check out my complete solution here:
» Full Solutions «
Like and subscribe too! =)
1. The coefficient of $ \ x^2 \ $ in the expansion of $ \ (4 + ax) {(1 + \frac{x}{2})}^{6} \ $ is $ \ 3$. Find the value of the constant $ \ a$.
$$\tag*{[4]} $$
2. The point $ \ M \ $ is the mid-point of the line joining the points $ \ (3, 7) \ $ and $ \ (−1, 1) $. Find the equation of the line through $ \ M \ $ which is parallel to the line $ \ \frac{x}{3} + \frac{y}{2} = 1 $.
$$\tag*{[4]} $$
3. A curve is such that $ \ \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{k}{\sqrt x} $, where $ \ k \ $ is a constant. The points $ \ P (1, −1) \ $ and $ \ Q (4, 4) \ $ lie on the curve. Find the equation of the curve.
$$\tag*{[4]} $$
4.
The diagram shows a circle with centre $ \ O \ $ and radius $ \ r \ $ cm. Points $ \ A \ $ and $ \ B \ $ lie on the circle and angle $ \ AOB = 2 \theta \ $ radians. The tangents to the circle at $ \ A \ $ and $ \ B \ $ meet at $ \ T \ $.
(i) Express the perimeter of the shaded region in terms of $ \ r \ $ and $ \ \theta $.
$$\tag*{[3]} $$
(ii) In the case where $ \ r = 5 \ $ and $ \ \theta = 1.2 $, find the area of the shaded region.
$$\tag*{[4]} $$
5. 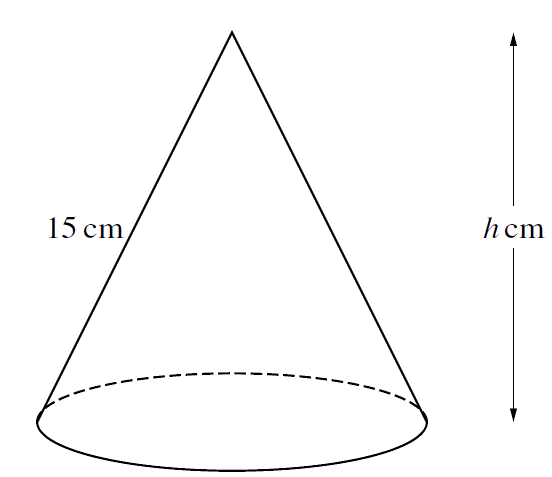
The diagram shows a solid cone which has a slant height of 15 cm and a vertical height of $ \ h \ $ cm.
(i) Show that the volume, $ \ V \ {\mathrm{cm}}^3$, of the cone is given by $ \ V = \frac{1}{3}\pi(225h − h^3)$.
[The volume of a cone of radius $ \ r \ $ and vertical height $ \ h \ $ is $ \ \frac{1}{3} \pi r^2 h $.]
$$\tag*{[2]} $$
(ii) Given that $ \ h \ $ can vary, find the value of $ \ h \ $ for which $ \ V \ $ has a stationary value. Determine, showing all necessary working, the nature of this stationary value.
$$\tag*{[5]} $$
6. (a) Given that $ \ x \gt 0 $, find the two smallest values of $ \ x $, in radians, for which $ \ 3 \tan (2x + 1) = 1 $. Show all necessary working.
$$\tag*{[4]} $$
(b) The function $ \ \mathrm{f} : x \mapsto 3 \ {\cos}^{2}x − 2 \ {\sin}^{2} x \ $ is defined for $ \ 0 \leq x \leq \pi $.
(i) Express $ \ \mathrm{f}(x) \ $ in the form $ \ a \ {\cos}^{2} x + b $, where $ \ a \ $ and $ \ b \ $ are constants.
$$\tag*{[1]} $$
(ii) Find the range of $ \ \mathrm{f} $.
$$\tag*{[1]} $$
7. 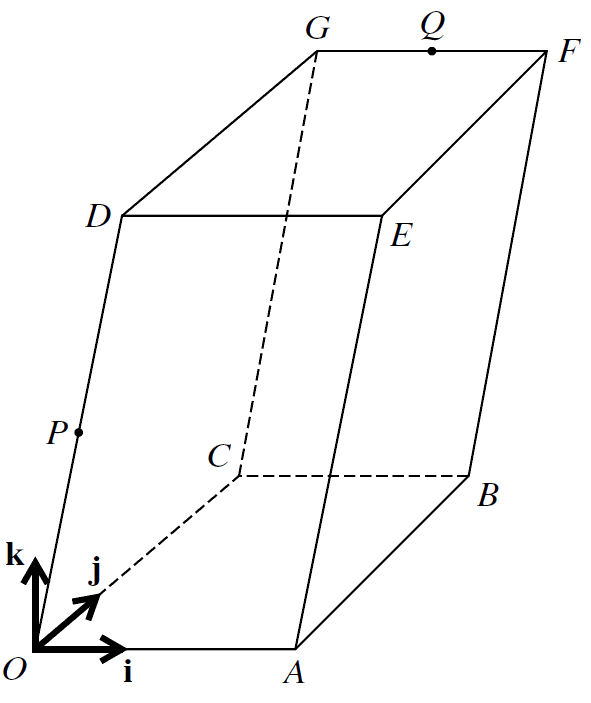
The diagram shows a three-dimensional shape $ \ OABCDEFG $. The base $ \ OABC \ $ and the upper surface $ \ DEFG \ $ are identical horizontal rectangles. The parallelograms $ \ OAED \ $ and $ \ CBFG \ $ both lie in vertical planes. Points $ \ P \ $ and $ \ Q \ $ are the mid-points of $ \ OD \ $ and $ \ GF \ $ respectively. Unit vectors $ \ \textbf{i} \ $ and $ \ \textbf{j} \ $ are parallel to $ \ \overrightarrow{OA} \ $ and $ \ \overrightarrow{OC} \ $ respectively and the unit vector $ \ \textbf{k} \ $ is vertically upwards. The position vectors of $ \ A \ $, $ \ C \ $ and $ \ D \ $ are given by $ \ \overrightarrow{OA} = 6\textbf{i}, \ \overrightarrow{OC} = 8\textbf{j} \ $ and $ \ \overrightarrow{OD} = 2\textbf{i} + 10\textbf{k} $.
(i) Express each of the vectors $ \ \overrightarrow{PB} \ $ and $ \ \overrightarrow{PQ} \ $ in terms of $ \ \textbf{i} $, $ \ \textbf{j} \ $ and $ \ \textbf{k} $.
$$\tag*{[4]} $$
(ii) Determine whether $ \ P \ $ is nearer to $ \ Q \ $ or to $ \ B $.
$$\tag*{[2]} $$
(iii) Use a scalar product to find angle $ \ BPQ$.
$$\tag*{[3]} $$
8. (a) Over a 21-day period an athlete prepares for a marathon by increasing the distance she runs each day by 1.2 km. On the first day she runs 13 km.
(i) Find the distance she runs on the last day of the 21-day period.
$$\tag*{[1]} $$
(ii) Find the total distance she runs in the 21-day period.
$$\tag*{[2]} $$
(b) The first, second and third terms of a geometric progression are $ \ x, x − 3 \ $ and $ \ x − 5 \ $ respectively.
(i) Find the value of $ \ x $.
$$\tag*{[2]} $$
(ii) Find the fourth term of the progression.
$$\tag*{[2]} $$
(ii) Find the sum to infinity of the progression.
$$\tag*{[2]} $$
9. Functions $ \ \mathrm{f} \ $ and $ \ \mathrm{g} \ $ are defined by
$$ \mathrm{f}(x) = 2x^2 + 8x + 1 \enspace \textrm{for} \ x \in \mathbb{R}, $$
$$ \mathrm{g}(x) = 2x \ – \ k \enspace \textrm{for} \ x \in \mathbb{R}, $$
where $ \ k \ $ is a constant.
(i) Find the value of $ \ k \ $ for which the line $ \ y = \mathrm{g}(x) \ $ is a tangent to the curve $ \ y = \mathrm{f}(x) $.
$$\tag*{[3]} $$
(ii) In the case where $ \ k = −9$, find the set of values of $ \ x \ $ for which $ \ \mathrm{f}(x) \lt \mathrm{g}(x) $.
$$\tag*{[4]} $$
(iii) In the case where $ \ k = -1 $, find $ \ {\mathrm{g}}^{−1}\mathrm{f}(x) \ $ and solve the equation $ \ {\mathrm{g}}^{−1}\mathrm{f}(x) = 0 $.
$$\tag*{[3]} $$
(iv) Express $ \ \mathrm{f}(x) \ $ in the form $ \ 2{(x + a)}^{2} + b $, where $ \ a \ $ and $ \ b \ $ are constants, and hence state the least value of $ \ \mathrm{f}(x) $.
$$\tag*{[3]} $$
10.
The diagram shows part of the curve $ \ y = 1 \ − \ {\large\frac{4}{{(2x \ + \ 1)}^{2}}} $. The curve intersects the $ \ x$-axis at $ \ A $. The normal to the curve at $ \ A \ $ intersects the $ \ y$-axis at $ \ B $.
(i) Obtain expressions for $ \ \frac{\mathrm{d}y}{\mathrm{d}x} \ $ and $ \int y \ \mathrm{d}x$.
$$\tag*{[4]} $$
(ii) Find the coordinates of $ \ B $.
$$\tag*{[4]} $$
(iii) Find, showing all necessary working, the area of the shaded region.
$$\tag*{[4]} $$
