Check out my complete solution here:
» Full Solutions «
Like and subscribe too! =)

1.     Two fair coins are thrown at the same time. The random variable $X$ is the number of throws of the two coins required to obtain two tails at the same time.

    (a)     Find the probability that two tails are obtained for the first time on the 7th throw.
$$\tag*{[2]} $$
    (b)     Find the probability that it takes more than 9 throws to obtain two tails for the first time.
$$\tag*{[2]} $$

2.     A summary of 40 values of $x$ gives the following information:
$$ \Sigma (x \ – \ k) = 520, \enspace \Sigma {(x \ – \ k)}^{2} = 9640, $$
    where $k$ is a constant.

    (a)     Given that the mean of these 40 values of $x$ is 34, find the value of $k$.
$$\tag*{[2]} $$
    (b)     Find the variance of these 40 values of $x$.
$$\tag*{[2]} $$

3.     For her bedtime drink, Suki has either chocolate, tea or milk with probabilities 0.45, 0.35 and 0.2 respectively. When she has chocolate, the probability that she has a biscuit is 0.3. When she has tea, the probability that she has a biscuit is 0.6. When she has milk, she never has a biscuit.

       Find the probability that Suki has tea given that she does not have a biscuit.
$$\tag*{[5]} $$

4.     A fair spinner has edges numbered 0, 1, 2, 2. Another fair spinner has edges numbered −1, 0, 1. Each spinner is spun. The number on the edge on which a spinner comes to rest is noted. The random variable $X$ is the sum of the numbers for the two spinners.

    (a)     Draw up the probability distribution table for $X$.
$$\tag*{[3]} $$
    (b)     Find $\mathrm{Var}(X)$.
$$\tag*{[3]} $$

5.     Raman and Sanjay are members of a quiz team which has 9 members in total. Two photographs of the quiz team are to be taken.

        For the first photograph, the 9 members will stand in a line.

    (a)     How many different arrangements of the 9 members are possible in which Raman will be at the centre of the line?
$$\tag*{[1]} $$

    (b)     How many different arrangements of the 9 members are possible in which Raman and Sanjay are
not next to each other?
$$\tag*{[3]} $$
   For the second photograph, the members will stand in two rows, with 5 in the back row and 4 in the front row.

    (c)     In how many different ways can the 9 members be divided into a group of 5 and a group of 4?
$$\tag*{[2]} $$

    (d)     For a random division into a group of 5 and a group of 4, find the probability that Raman and Sanjay are in the same group as each other.
$$\tag*{[4]} $$

6.     The weights, in kg, of 15 rugby players in the Rebels club and 15 soccer players in the Sharks club are shown below.
   

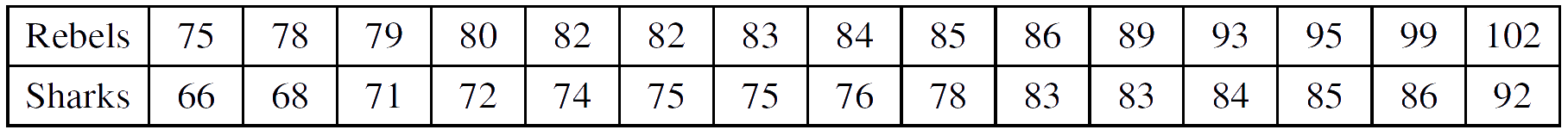
    (a)     Represent the data by drawing a back-to-back stem-and-leaf diagramwith Rebels on the left-hand side of the diagram.
$$\tag*{[4]} $$
        (b)     Find the median and the interquartile range for the Rebels.
$$\tag*{[3]} $$
        A box-and-whisker plot for the Sharks is shown below.

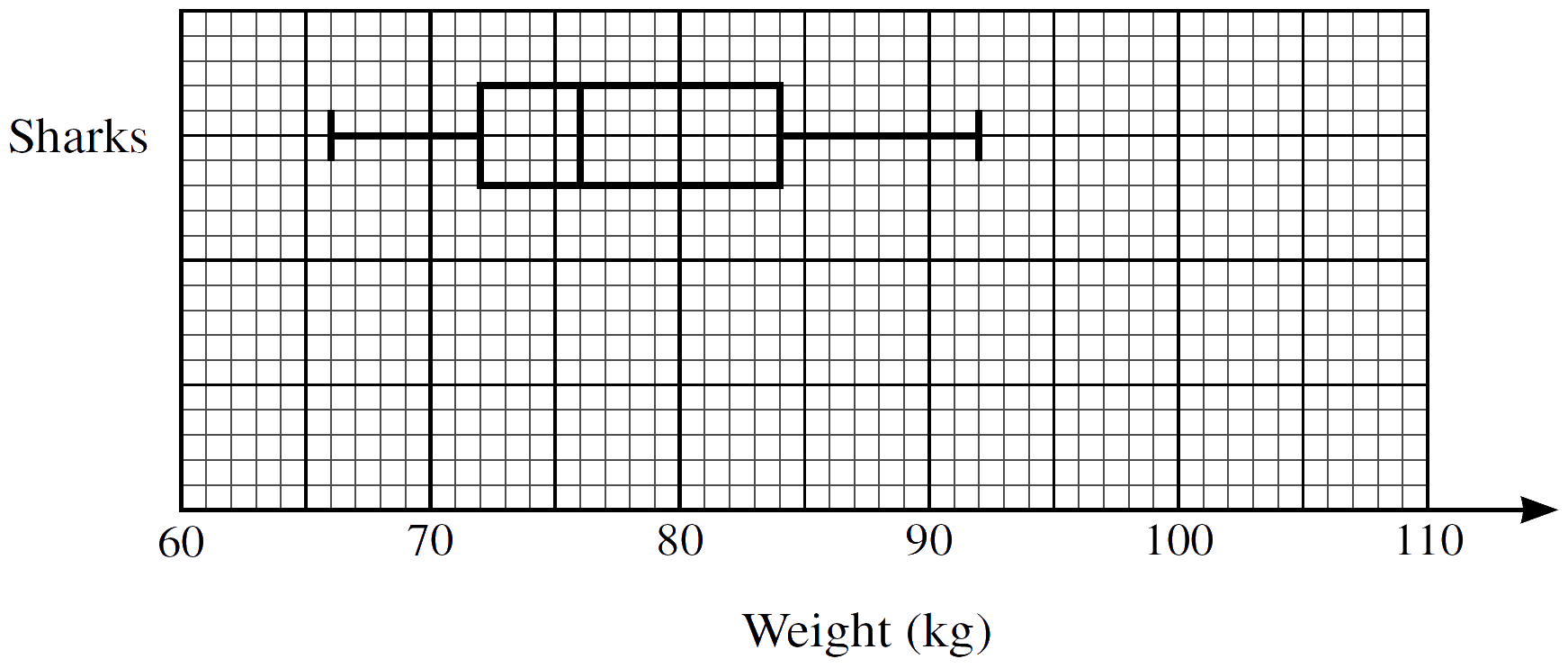
        (c)     On the same diagram, draw a box-and-whisker plot for the Rebels.
$$\tag*{[2]} $$

        (d)     Make one comparison between the weights of the players in the Rebels club and the weights of the players in the Sharks club.
$$\tag*{[1]} $$

7.     The times, in minutes, that Karli spends each day on social media are normally distributed with mean 125 and standard deviation 24.

    (a)     (i)     On how many days of the year (365 days) would you expect Karli to spend more than 142 minutes on social media?
$$\tag*{[5]} $$
        (ii)     Find the probability that Karli spends more than 142 minutes on social media on fewer than 2 of 10 randomly chosen days.
$$\tag*{[3]} $$
       On 90% of days, Karli spends more than $t$ minutes on social media.

    (b)     Find the value of $t$.
$$\tag*{[3]} $$