Check out my complete solution here:
» Full Solutions «
Like and subscribe too! =)

1.     (a)     Express $16x^2 \ − \ 24x \ + \ 10 $ in the form $(4x + a)^2 \ + \ b$.
$$\tag*{[2]} $$
        (b)     It is given that the equation $16x^2 \ − \ 24x \ + \ 10 = k$ where $k$ is a constant, has exactly one root. Find the value of this root.
$$\tag*{[2]} $$

2.     (a)     The graph of $y = \mathrm{f}(x)$ is transformed to the graph of $y = 2\mathrm{f}(x \ – \ 1)$.

        Describe fully the two single transformations which have been combined to give the resulting transformation.
$$\tag*{[3]} $$
        (b)     The curve $ y = \sin 2x − 5x $ is reflected in the $y$-axis and then stretched by scale factor $\frac{1}{3}$ in the $x$-direction.

        Write down the equation of the transformed curve.
$$\tag*{[2]} $$

3.     The equation of a curve is $y = (x \ − \ 3)\sqrt{ x \ + \ 1} \ + \ 3$. The following points lie on the curve. Non-exact values are rounded to 4 decimal places.

$$ A (2, k) \enspace B(2.9, 2.8025) \enspace C (2.99, 2.9800) $$

$$ D (2.999, 2.9980) \enspace E (3, 3) $$

    (a)     Find $k$, giving your answer correct to 4 decimal places.
$$\tag*{[1]} $$
    (b)     Find the gradient of $AE$, giving your answer correct to 4 decimal places.
$$\tag*{[1]} $$
    The gradients of $BE$, $CE$ and $DE$, rounded to 4 decimal places, are 1.9748, 1.9975 and 1.9997 respectively.

    (c)     State, giving a reason for your answer, what the values of the four gradients suggest about the gradient of the curve at the point $E$.
$$\tag*{[2]} $$

4.     The coefficient of $x$ in the expansion of $ {\Big ( 4x \ + \ \frac{10}{x} \Big )}^{3} $ is $p$. The coefficient of $\frac{1}{x}$ in the expansion of $ {\Big ( 2x \ + \ \frac{k}{x^2} \Big )}^{5} $ is $q$.

    Given that $p = 6q$, find the possible values of $k$.
$$\tag*{[5]} $$

5.     The function $ \ \mathrm{f} \ $ is defined by $ \ \mathrm{f}(x) = 2x^2 \ + \ 3 $ for $ x \ge 0$.

    (a)     Find and simplify an expression for $ \ \mathrm{f}\mathrm{f}(x) $ .
$$\tag*{[2]} $$
    (b)     Solve the equation $ \ \mathrm{f}\mathrm{f}(x) = 34x^2 \ + \ 19 $ .
$$\tag*{[4]} $$

6.     Points $A$ and $B$ have coordinates $(8, 3)$ and $(p, q)$ respectively. The equation of the perpendicular bisector of $AB$ is $y = −2x \ + \ 4$.

    Find the values of $p$ and $q$.
$$\tag*{[4]} $$

7.     The point $A$ has coordinates $(1, 5)$ and the line $l$ has gradient $ – \frac{2}{3}$ and passes through $A$. A circle has centre $(5, 11)$ and radius $\sqrt{52}$.

    (a)     Show that l is the tangent to the circle at A.
$$\tag*{[2]} $$
    (b)     Find the equation of the other circle of radius $\sqrt{52}$ for which $l$ is also the tangent at $A$.
$$\tag*{[3]} $$

8.     The first, second and third terms of an arithmetic progression are $a, \frac{3}{2}a$ and $b$ respectively, where $a$ and $b$ are positive constants. The first, second and third terms of a geometric progression are $a$, 18 and $b$ + 3 respectively.

    (a)     Find the values of a and b.
$$\tag*{[5]} $$
    (b)     Find the sum of the first 20 terms of the arithmetic progression.
$$\tag*{[3]} $$

9.    

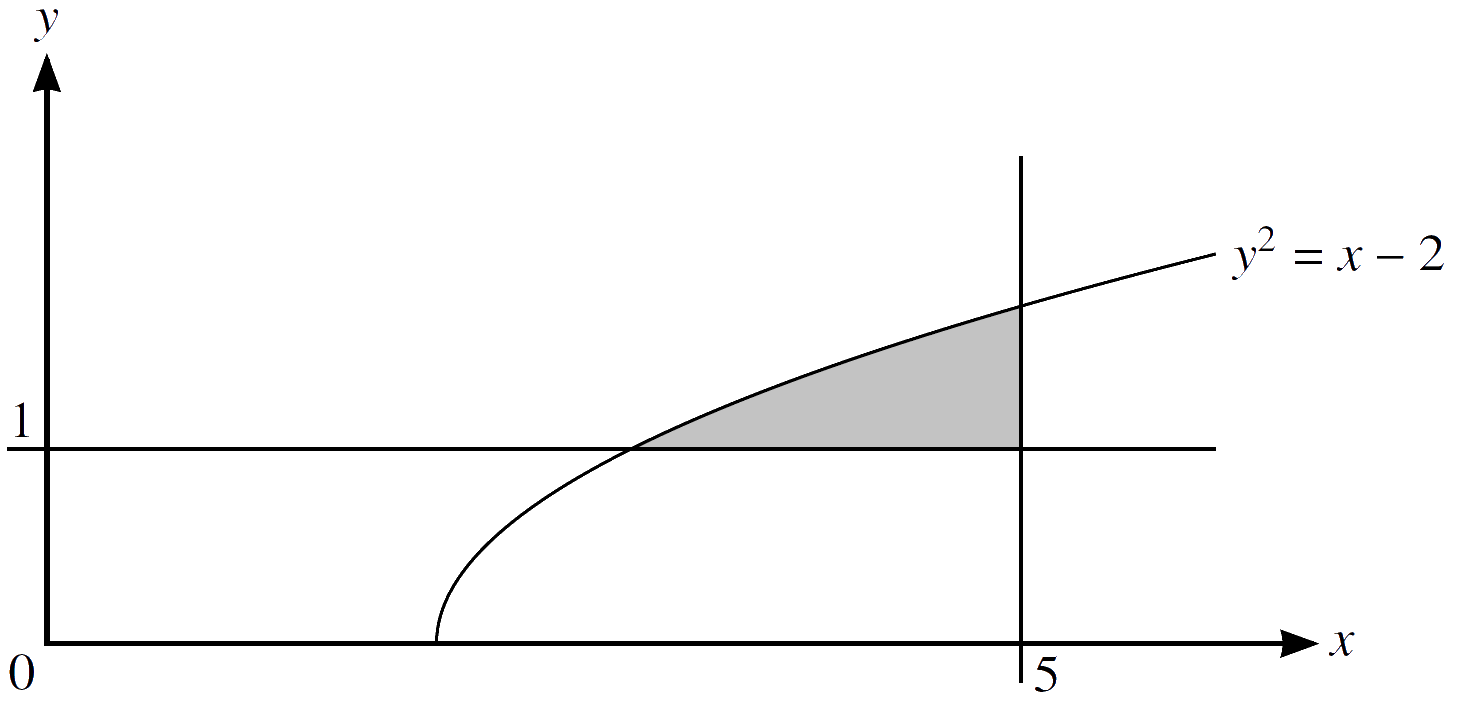
    The diagram shows part of the curve with equation $y^2 = x − 2$ and the lines $x = 5$ and $y = 1$. The shaded region enclosed by the curve and the lines is rotated through ${360}^{\circ}$ about the $x$-axis. Find the volume obtained.
$$\tag*{[6]} $$

10.     (a)     Prove the identity $ \frac{ 1 \ + \ \sin x }{ 1 \ – \ \sin x} – \frac{ 1 \ – \ \sin x }{ 1 \ + \ \sin x } \equiv \frac{ 4 \tan x }{ \cos x } $.
$$\tag*{[4]} $$
        (b)     Hence solve the equation $ \frac{ 1 \ + \ \sin x }{ 1 \ – \ \sin x} – \frac{ 1 \ – \ \sin x }{ 1 \ + \ \sin x } = 8 \tan x$ for $ 0 \le x \le \frac{1}{2} \pi$.
$$\tag*{[3]} $$

11.     The gradient of a curve is given by $ \frac{\mathrm{d}y}{\mathrm{d}x} = 6{(3x \ − \ 5)}^{3} − k{x}^{2}$, where $k$ is a constant. The curve has a stationary point at $(2, −3.5)$.

    (a)     Find the value of $k$.
$$\tag*{[2]} $$
    (b)     Find the equation of the curve.
$$\tag*{[4]} $$
    (c)     Find $ \ \frac{{\mathrm{d}}^{2}y}{{\mathrm{d}}^{2}x} $.
$$\tag*{[2]} $$
    (d)     Determine the nature of the stationary point at $(2, −3.5)$.
$$\tag*{[2]} $$

12.    

    The diagram shows a cross-section of seven cylindrical pipes, each of radius 20 cm, held together by a thin rope which is wrapped tightly around the pipes. The centres of the six outer pipes are $A$, $B$, $C$, $D$, $E$ and $F$. Points $P$ and $Q$ are situated where straight sections of the rope meet the pipe with centre $A$.

    (a)     Show that angle $PAQ = \frac{1}{3}\pi$ radians.
$$\tag*{[2]} $$
    (b)     Find the length of the rope.
$$\tag*{[4]} $$
    (c)     Find the area of the hexagon $ABCDEF$, giving your answer in terms of $\sqrt{3}$.
$$\tag*{[2]} $$
    (d)     Find the area of the complete region enclosed by the rope.
$$\tag*{[3]} $$