1. The times, $t$ seconds, taken to swim 100 m were recorded for a group of 9 swimmers and were found to be as follows.
\begin{align*}
95 \quad 126 \quad 117 \quad 135 \quad 120 \\[2ex]
125 \quad 114 \quad 119 \quad 136
\end{align*}
(i) Find the values of $\sum (t − 120) \ $ and $ \ \sum {(t − 120)}^{2}$.
$$\tag*{[2]} $$
(ii) Using your values found in part (i), calculate the variance of $t$.
$$\tag*{[2]} $$
2. Jameel has 5 plums and 3 apricots in a box. Rosa has $x$ plums and 6 apricots in a box. One fruit is chosen at random from Jameel’s box and one fruit is chosen at random from Rosa’s box. The probability that both fruits chosen are plums is $\frac{1}{4}$. Write down an equation in $x$ and hence find $x$.
$$\tag*{[3]} $$
3. A fair six-sided die is thrown twice and the scores are noted. Event $X$ is defined as ‘The total of the two scores is 4’. Event $Y$ is defined as ‘The first score is 2 or 5’. Are events $X$ and $Y$ independent? Justify your answer.
$$\tag*{[4]} $$
4. The Mathematics and English A-level marks of 1400 pupils all taking the same examinations are shown in the cumulative frequency graphs below. Both examinations are marked out of 100.
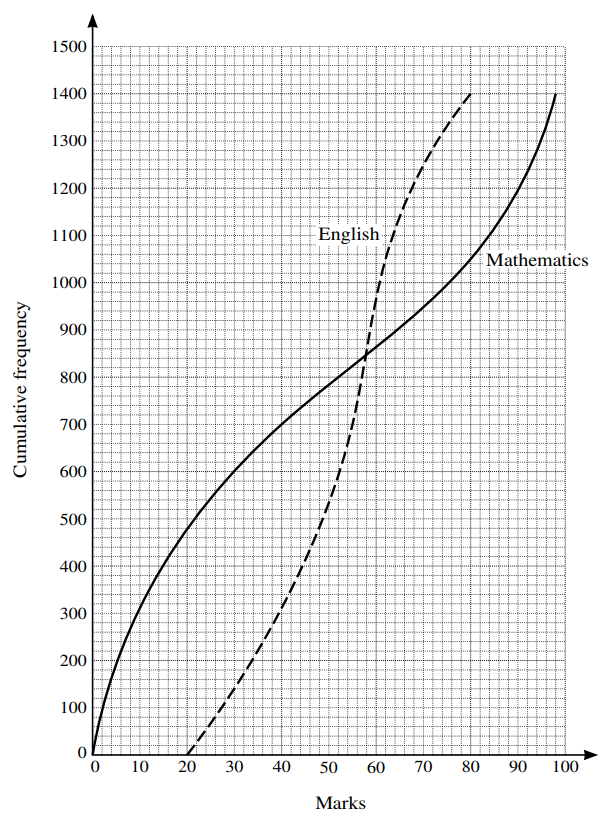
Use suitable data from these graphs to compare the central tendency and spread of the marks in Mathematics and English.
$$\tag*{[6]} $$
5. In a certain country the probability that a child owns a bicycle is 0.65.
(i) A random sample of 15 children from this country is chosen. Find the probability that more than 12 own a bicycle.
$$\tag*{[3]} $$
(b) A random sample of 250 children from this country is chosen. Use a suitable approximation to find the probability that fewer than 179 own a bicycle.
$$\tag*{[4]} $$
6. At a funfair, Amy pays \$1 for two attempts to make a bell ring by shooting at it with a water pistol.
$ \enspace \bullet \ $ If she makes the bell ring on her first attempt, she receives \$3 and stops playing. This means that overall she has gained \$2.
$ \enspace \bullet \ $ If she makes the bell ring on her second attempt, she receives \$1.50 and stops playing. This means that overall she has gained \$0.50.
$ \enspace \bullet \ $ If she does not make the bell ring in the two attempts, she has lost her original \$1.
The probability that Amy makes the bell ring on any attempt is 0.2, independently of other attempts.
(i) Show that the probability that Amy loses her original \$1 is 0.64.
$$\tag*{[2]} $$
(ii) Complete the probability distribution table for the amount that Amy gains.
$$\tag*{[4]} $$
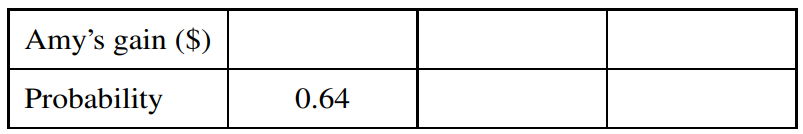
(iii) Calculate Amy’s expected gain.
$$\tag*{[1]} $$
7. The weight of adult female giraffes has a normal distribution with mean 830 kg and standard deviation 120 kg.
(i) There are 430 adult female giraffes in a particular game reserve. Find the number of these adult female giraffes which can be expected to weigh less than 700 kg.
$$\tag*{[4]} $$
(ii) Given that 90% of adult female giraffes weigh between $ \ (830 − w) \ $ kg and $ \ (830 + w) \ $ kg, find the value of $w$.
$$\tag*{[4]} $$
The weight of adult male giraffes has a normal distribution with mean 1190 kg and standard deviation $\sigma$ kg.
(iii) Given that 83.4% of adult male giraffes weigh more than 950 kg, find the value of $\sigma$. [3]
$$\tag*{[3]} $$
8. Freddie has 6 toy cars and 3 toy buses, all different. He chooses 4 toys to take on holiday with him.
(i) In how many different ways can Freddie choose 4 toys?
$$\tag*{[1]} $$
(ii) How many of these choices will include both his favourite car and his favourite bus?
$$\tag*{[2]} $$
Freddie arranges these 9 toys in a line.
(iii) Find the number of possible arrangements if the buses are all next to each other.
$$\tag*{[3]} $$
(iv) Find the number of possible arrangements if there is a car at each end of the line and no buses are next to each other.
$$\tag*{[3]} $$
