Check out my complete solution here:
» Full Solutions «
Like and subscribe too! =)
1. (a) Find the coefficient of $ \ x^2 \ $ in the expansion of $ \ {(x \ – \ \frac{2}{x})}^{6} $.
$$\tag*{[2]} $$
(b) Find the coefficient of $ \ x^2 \ $ in the expansion of $ \ (2 + 3{x}^{2}){(x \ – \ \frac{2}{x})}^{6} $.
$$\tag*{[3]} $$
2. (a) Express the equation $ \ 3 \cos \theta = 8 \tan \theta \ $ as a quadratic equation in $ \ \sin \theta $.
$$\tag*{[3]} $$
(b) Hence find the acute angle, in degrees, for which $ \ 3 \cos \theta = 8 \tan \theta $.
$$\tag*{[2]} $$
3. A weather balloon in the shape of a sphere is being inflated by a pump. The volume of the balloon is increasing at a constant rate of $ \ 600 \ {\mathrm{cm}}^{3} \ $ per second. The balloon was empty at the start of pumping.
(a) Find the radius of the balloon after 30 seconds.
$$\tag*{[2]} $$
(b) Find the rate of increase of the radius after 30 seconds.
$$\tag*{[3]} $$
4. The $ \ n$th term of an arithmetic progression is $ \ \frac{1}{2}(3n \ – \ 15) $.
Find the value of $ \ n \ $ for which the sum of the first $ \ n \ $ terms is 84.
$$\tag*{[5]} $$
5. The function $ \ \mathrm{f} \ $ is defined for $ \ x \in \mathbb{R} \ $ by
$$ \ \mathrm{f} : x \mapsto \ a \ – \ 2x, $$
where $ \ a \ $ is a constant.
(a) Express $ \ \mathrm{f}\mathrm{f}(x) \ $ and $ \ {\mathrm{f}}^{-1}(x) \ $ in terms of $ \ a \ $ and $ \ x $.
$$\tag*{[4]} $$
(b) Given that $ \ \mathrm{f}\mathrm{f}(x) = {\mathrm{f}}^{-1}(x) $, find $ \ x \ $ in terms of $ \ a $.
$$\tag*{[2]} $$
6. The equation of a curve is $ \ y = 2x^2 + kx + k \ − \ 1 $, where $ \ k \ $ is a constant.
(a) Given that the line $ \ y = 2x + 3 \ $ is a tangent to the curve, find the value of $ \ k $.
$$\tag*{[3]} $$
It is now given that $ \ k = 2 $.
(b) Express the equation of the curve in the form $ \ y = 2{(x + a)}^{2} + b $, where $ \ a \ $ and $ \ b \ $ are constants, and hence state the coordinates of the vertex of the curve.
$$\tag*{[3]} $$
7. 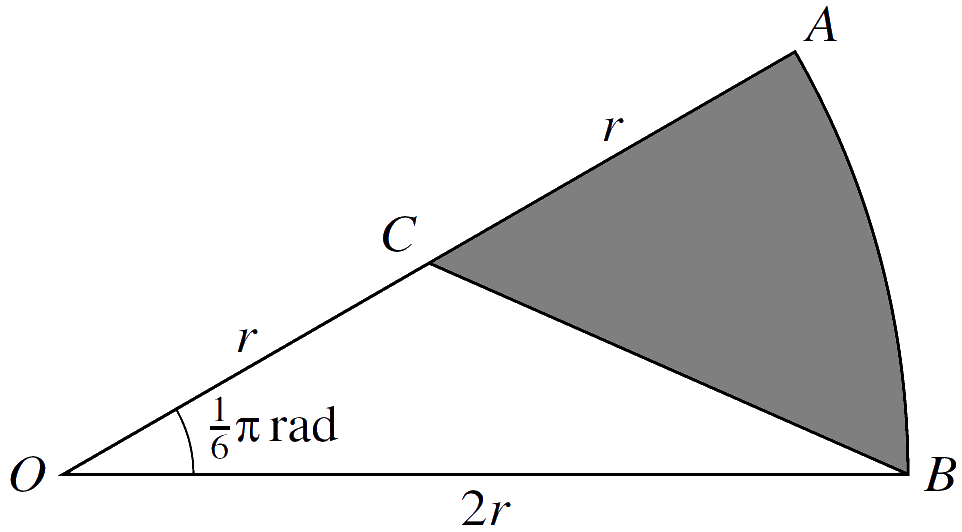
In the diagram, $ \ OAB \ $ is a sector of a circle with centre $ \ O \ $ and radius $ \ 2r $, and angle $ \ AOB = \frac{1}{6} \pi \ $ radians. The point $ \ C \ $ is the midpoint of $ \ OA $.
(a) Show that the exact length of $ \ BC \ $ is $ \ r \sqrt{5 \ – \ 2 \sqrt{3}} $.
$$\tag*{[2]} $$
(b) Find the exact perimeter of the shaded region.
$$\tag*{[2]} $$
(c) Find the exact area of the shaded region.
$$\tag*{[3]} $$
8. 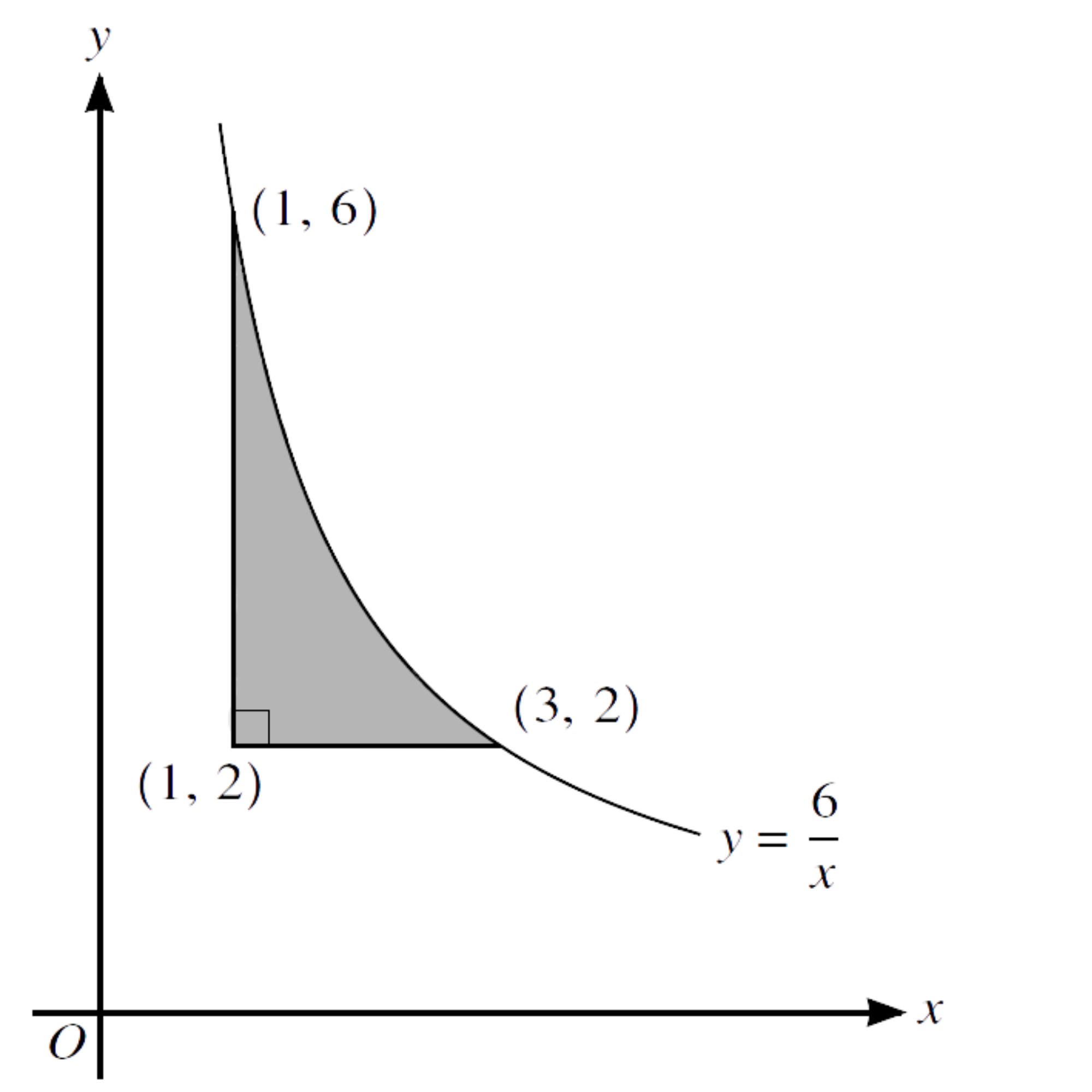
(a) Find the volume generated when the shaded region is rotated through $ \ {360}^{\circ} \ $ about the $ \ \textbf{y-axis} $.
$$\tag*{[5]} $$
(b) The tangent to the curve at a point $ \ X \ $ is parallel to the line $ \ y + 2x = 0 $. Show that $ \ X \ $ lies on the line $ \ y = 2x $.
$$\tag*{[3]} $$
9. Functions $ \ \mathrm{f} \ $ and $ \ \mathrm{g} \ $ are such that
$$ \mathrm{f}(x) = 2 \ – \ 3 \sin 2x \enspace \textrm{for} \ 0 \le x \le \pi, $$
$$ \mathrm{g}(x) = -2 \mathrm{f}(x) \enspace \textrm{for} \ 0 \le x \le \pi. $$
(a) State the ranges of $ \ \mathrm{f} \ $ and $ \ \mathrm{g} $.
$$\tag*{[3]} $$
The diagram below shows the graph of $ \ y = f(x) $.
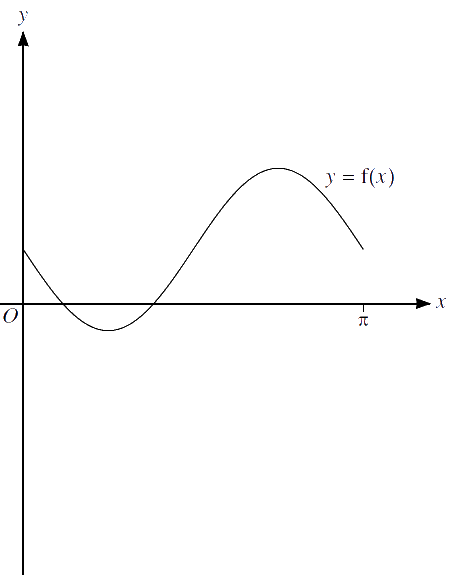
(b) Sketch, on this diagram, the graph of $ \ y = g(x) $.
$$\tag*{[2]} $$
The function $ \ \mathrm{h} \ $ is such that
$$ \mathrm{h}(x) = \mathrm{g}(x+\pi) \enspace \textrm{for} \ -\pi \le x \le 0. $$
(c) Describe fully a sequence of transformations that maps the curve $ \ y = f(x) \ $ on to $ \ y = h(x) $.
$$\tag*{[3]} $$
10. The equation of a curve is $ \ y = 54x \ − \ {(2x − 7)}^{3} $.
(a) Find $ \ \frac{\mathrm{d}y}{\mathrm{d}x} \ $ and $ \ \frac{{\mathrm{d}}^{2}y}{{\mathrm{d}}^{2}x} $.
$$\tag*{[4]} $$
(b) Find the coordinates of each of the stationary points on the curve.
$$\tag*{[3]} $$
(c) Determine the nature of each of the stationary points.
$$\tag*{[2]} $$
11. The equation of a circle with centre $ \ C \ $ is $ \ x^2 + y^2 − 8x + 4y − 5 = 0 $.
(a) Find the radius of the circle and the coordinates of $ \ C $.
$$\tag*{[3]} $$
The point $ \ P(1, 2) \ $ lies on the circle.
(b) Show that the equation of the tangent to the circle at $ \ P \ $ is $ \ 4y = 3x + 5 $.
$$\tag*{[3]} $$
The point $ \ Q \ $ also lies on the circle and $ \ PQ \ $ is parallel to the $ \ x $-axis.
(c) Write down the coordinates of $ \ Q $.
$$\tag*{[2]} $$
The tangents to the circle at $ \ P \ $ and $ \ Q \ $ meet at $ \ T $.
(d) Find the coordinates of $ \ T $.
$$\tag*{[3]} $$
