Check out my complete solution here:
» Full Solutions «
Like and subscribe too! =)
1. The heights in cm of 160 sunflower plants were measured. The results are summarised on the following cumulative frequency curve.
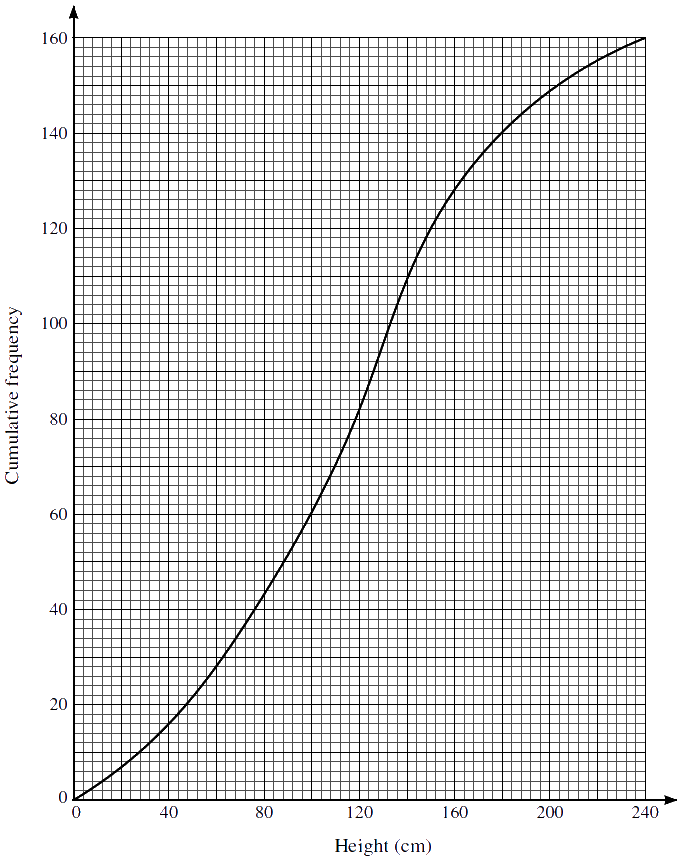
(a) Use the graph to estimate the number of plants with heights less than 100 cm.
$$\tag*{[1]} $$
(b) Use the graph to estimate the 65th percentile of the distribution.
$$\tag*{[2]} $$
(c) Use the graph to estimate the interquartile range of the heights of these plants.
$$\tag*{[2]} $$
2. The random variable $X$ can take only the values −2, −1, 0, 1, 2. The probability distribution of $X$ is given in the following table.
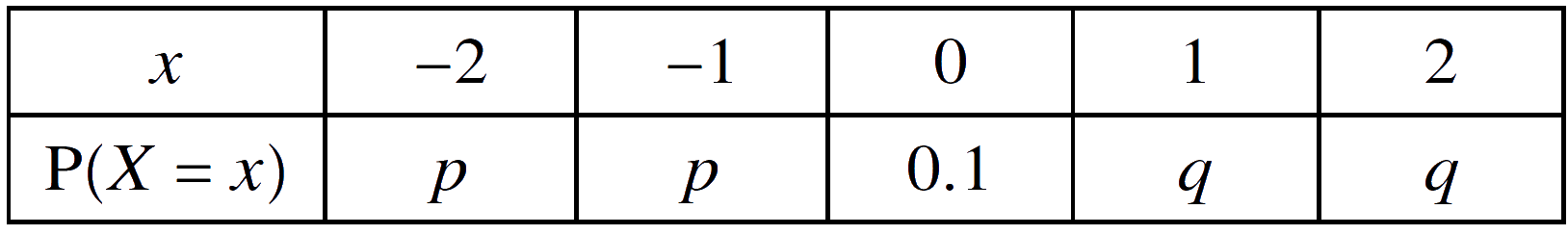
Given that $\mathrm{P}(X \ge 0) = 3\mathrm{P}(X \lt 0)$, find the values of $p$ and $q$.
$$\tag*{[4]} $$
3. A sports club has a volleyball team and a hockey team. The heights of the 6 members of the volleyball team are summarised by $\Sigma x = 1050$ and $\Sigma x^2 = 193 700$, where $x$ is the height of a member in cm. The heights of the 11 members of the hockey team are summarised by $\Sigma y = 1991$ and $\Sigma y^2 = 366 400$, where $y$ is the height of a member in cm.
(a) Find the mean height of all 17 members of the club.
$$\tag*{[2]} $$
(b) Find the standard deviation of the heights of all 17 members of the club.
$$\tag*{[3]} $$
4. Three fair six-sided dice, each with faces marked 1, 2, 3, 4, 5, 6, are thrown at the same time, repeatedly. For a single throw of the three dice, the score is the sum of the numbers on the top faces.
(a) Find the probability that the score is 4 on a single throw of the three dice.
$$\tag*{[3]} $$
(b) Find the probability that a score of 18 is obtained for the first time on the 5th throw of the three dice.
$$\tag*{[3]} $$
5. The lengths of the leaves of a particular type of tree are modelled by a normal distribution. A scientist measures the lengths of a random sample of 500 leaves from this type of tree and finds that 42 are less than 4 cm long and 100 are more than 10 cm long.
(a) Find estimates for the mean and standard deviation of the lengths of leaves from this type of tree.
$$\tag*{[5]} $$
The lengths, in cm, of the leaves of a different type of tree have the distribution $N(\mu, \sigma^2)$. The scientist takes a random sample of 800 leaves from this type of tree.
(b) Find how many of these leaves the scientist would expect to have lengths, in cm, between $ \mu \ – \ 2\sigma$ and $ \mu \ – \ 2\sigma$.
$$\tag*{[4]} $$
6. (a) How many different arrangements are there of the 11 letters in the word REQUIREMENT?
$$\tag*{[2]} $$
(b) How many different arrangements are there of the 11 letters in the word REQUIREMENT in which the two Rs are together and the three Es are together?
$$\tag*{[1]} $$
(c) How many different arrangements are there of the 11 letters in the word REQUIREMENT in which there are exactly three letters between the two Rs?
$$\tag*{[3]} $$
Five of the 11 letters in the word REQUIREMENT are selected.
(d) How many possible selections contain at least two Es and at least one R?
$$\tag*{[4]} $$
7. In the region of Arka, the total number of households in the three villages Reeta, Shan and Teber is 800. Each of the households was asked about the quality of their broadband service. Their responses are summarised in the following table.
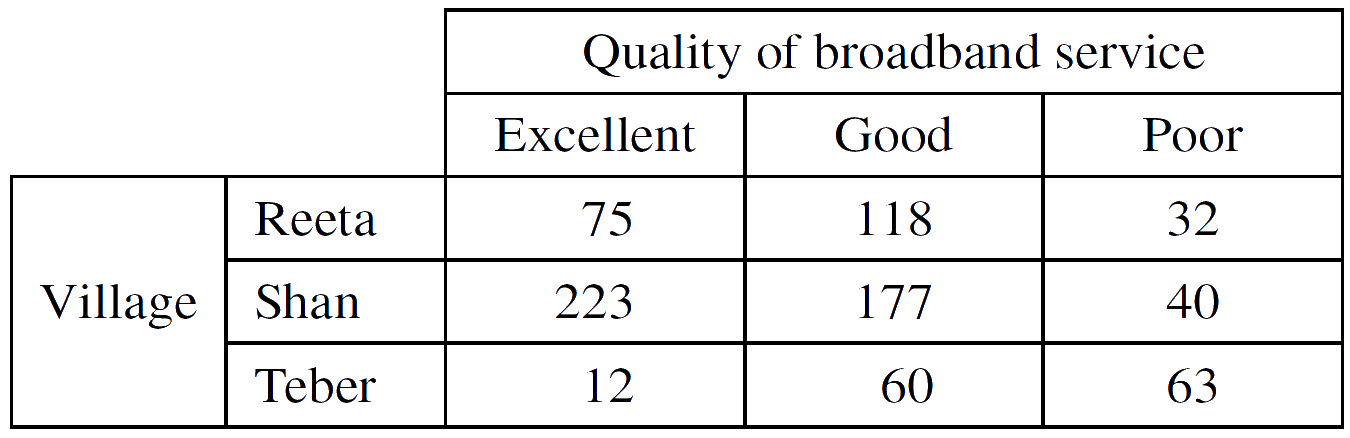
(a) (i) Find the probability that a randomly chosen household is in Shan and has poor broadband service.
$$\tag*{[1]} $$
(ii) Find the probability that a randomly chosen household has good broadband service given that the household is in Shan.
$$\tag*{[2]} $$
In the whole of Arka there are a large number of households. A survey showed that 35% of households in Arka have no broadband service.
(b) (i) 10 households in Arka are chosen at random. Find the probability that fewer than 3 of these households have no broadband service.
$$\tag*{[3]} $$
(ii) 120 households in Arka are chosen at random. Use an approximation to find the probability that more than 32 of these households have no broadband service.
$$\tag*{[5]} $$
